传统方法允许通过简单支撑梁的均衡模型,基于由一个或两个轴承支撑的单个轴来估计应用中的轴承载荷,该方法是快速选择轴承的理想方法,通过对轴几何结构和操作条件的最少信息,可以评估轴承负载,以适应广泛的应用。
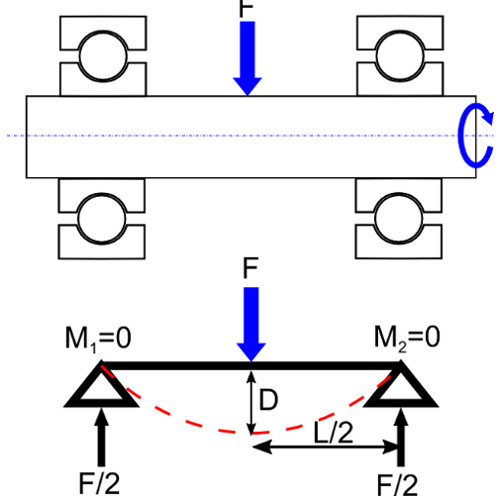

在上图所示的示例中,传统方法可以快速提供每个支架承载的施加载荷(F)的大小,超静态结构(由两个以上轴承支撑的轴)不易处理,需要更复杂的模型来评估施加到不同支撑中的力的分布。
在这种方法中,一个主要假设是轴承相对于径向位移是无限刚性的,并且它们不提供旋转阻力,由于不需要轴承的内部几何形状,因此假设加载的滚动元件覆盖约180度的载荷区,而无需进一步详细计算。
传统方法对轴承刚度(=位移和旋转阻力)的假设有时候并不精确,并非所有轴承类型都适合大旋转或大轴向偏移,为了更好地了解轴承的性能,了解其内部几何结构非常重要。
轴承刚度是轴承箱方法中考虑的基本问题之一,最终平衡取决于几个组合刚度贡献,即轴、壳体和轴承,由于每一个千分尺都计数,因此轴承性能的准确评估也取决于实际操作条件,尤其是转速和温度,此外,用于将轴承固定在轴上和壳体座内部的配合也是一个极其重要的因素,配合、转速和温度从最初的轴承制造间隙严重改变为运行间隙(另见间隙减小)。
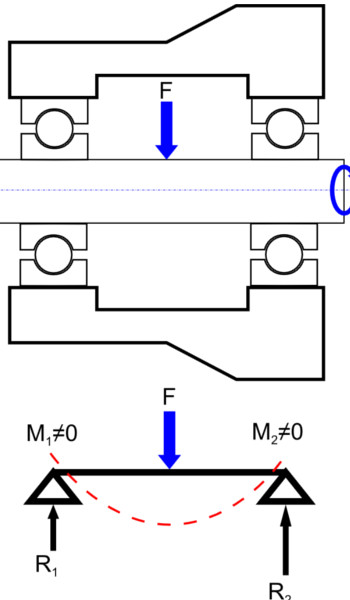

如上图所示,通过考虑轴承的真实内部几何形状以及轴和壳体的几何形状和安装配合,这种系统的解决方案不是传统方法所建议的,不同的壳体几何形状和可能的配合,右轴承可能会填充更大的间隙减小;工作内部间隙不同,左右轴承可能呈现不同的刚度;滚珠轴承提供的有限旋转刚度,轴承产生弯曲力矩;内部间隙不同,即使负载位于轴的中间,轴承负载条件也可能不同。


